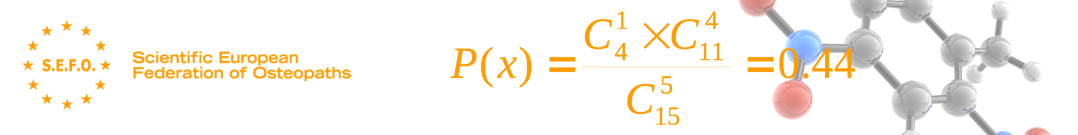Le statistiche

 

STATISTICA DESCRITTIVA Descrive – ordina un nsieme di dati che sono grezzi.	STATISTICA INFERENZIALE Permette di conoscere se le relazioni osservate in un campione possano occorrere nella popolazione generale. Valuta la variabilità aleatoria e controlla i fattori di confusione.
MISURAZIONE DELLA TENDENZA CENTRALE Media. Moda. Mediana. Intervallo di confidenza.	MISURAZIONE DELLA DISPERSIONE Deviazione standard. Range. Varianza.
STUDIO SPERIMENTALE Cerca differenze tra due o più insiemi di dati.	STUDIO DI CORRELAZIONE Cerca similitudini tra due o più insiemi di dati.

COSA DEVONO MISURARE LE STATISTICHE

1º MEDIA:

Media della popolazione da cui provengono i campioni.

2º DEVIAZIONE STANDARD: σ o s

Sono misure della dispersione dei valori della variabile nella popolazione e nel campione, rispettivamente.

È una statistica utilizzata come misura della dispersione o di variazione della distribuzione, uguale alla radice quadrata della media aritmetica dei quadrati delle deviazioni dalla media aritmetica.

• Misura della dispersione di un gruppo di dati a partire dalla loro media. Maggiore è la differenza tra i dati, più alta sarà la deviazione.
• Ha le stesse unità della variabile. La deviazione tipica non varia rispetto all’origine della distribuzione.

La deviazione standard si può anche calcolare come la radice quadrata della variazione.

3º INTERVALLO DI CONFIDENZA:

è un range di valori entro il quale si incontra il vero valore di un parametro o stima di un insieme di valori.

Permette di conoscere la precisione dello studio.

Differenti campioni porteranno a risultati differenti: abbiamo bisogno di una misurazione della precisione di questa stima, cosa che viene ottenuta con il calcolo dell’intervallo di confidenza (IC=95%).

Non si può indicare una variabile senza il proprio intervallo di confidenza, valore che determina la precisione (95% è molto buono, si lascia sempre un 5% di errore).

4º STANDARD D’ORO o “GOLD STANDARD”:

Test riconosciuto come riferimento standard o di diagnosi per una particolare malattia.

5º Sensibilità: tasso di veri positivi.

La probabilità del test di riscontrare una malattia tra i soggetti che hanno la malattia o la proporzione di persone con malattia che danno un risultato positivo al test.

Sensibilità = veri positivi / (veri positivi falsi negativi)

Riferendosi ad un test diagnostico, è la proporzione di persone veramente malate che sono state catalogate come tali grazie a detto test.

6º Specificità:

è la probabilità che il test non introntri NESSUNA malattia tra i soggetti che non hanno la malattia o la proporzione di persone senza malattia che danno un test negativo.

Specificità = veri negativi/ (veri negativi + falsi positivi)

7º Distribuzione normale: n.

Una distribuzione di frequenza teorica per un sistema di dati variabili, rappresentato generalmente da una curva a campana di Gauss simmetrica sul punto medio.

8º TENDENZA CENTRALE:

è il centro di una distribuzione. Descritto con media, punto medio e moda.

• Media: la media aritmetica in un sistema di valori. Il promedio. È una misura della centralizzazione per una variabile continua. Si ottiene sommando tutti i valori del campione e dividendo per la grandezza del campione.
• Mediana: per un sistema di valori disposti in ordine di grandezza, la mediana è il valore medio per i numeri dispari di valore e il promedio dei due valori medi per un numero pari. In una popolazione o campione, è il valore che occupa la posizione centrale quando tutti i valori si dispongono in un ordine decrescente (dal maggiore al minore). In una distribuzione normale, la mediana corrisponde al percentile 50%. La maediana fa in modo che si abbia un 50% di valori del campione inferiori a tale valore ed un 50% di valori del campione superiori a tale valore.
• Moda: per un sistema di valori, in una popolazione è il valore più frequente di una serie di osservazioni. È il valore che più si ripete in una variabile nominale.

9º INCIDENZA:

La incidenza riflette il numero di nuovi “casi” in un periodo di tempo.

È un indice dinamico che richiede un follow up della popolazione di interesse.

Si può misurare con due indici: incidenza accumulata e densità 8° tasso) di incidenza.

L’incidenza accumulata è la proporzione di individui che sviluppano l’evento durante il periodo di osservazione.

Tasso di incidenza

Numero di nuovi casi di una malattia o altri avvenimenti durante un periodo determinato, diviso per il numero di persone esposte al rischio durante questo periodo.

 10º PREVALENZA:

è la proporzione di individui di una popolazione che presentano l’evento in un momento, o periodo di tempo, determinato. Numero di casi di una malattia in una popolazione in un momento dato.

Per esempio: la prevalenza di diabete a Madrid nel 2001 è la proporzione di individui di questa provincia que nel 2001 soffrivano di questa malattia.

Tasso di prevalenza.

Numero totale di individui che presentano una caratteristica o soffrono di una patologia in un momento o periodo determinato, diviso per la popolazione a rischio di avere una caratteristica o patologia in quel momento o in corrispondenza della metà del periodo considerato.

11º VARIANZA:

Misura la dispersione delle variabili attorno alla media.

Valore atteso o aspettativa matematica o media.

Misura della variazione di una serie di osservazioni; è pari alla somma dei quadrati delle deviazioni rispetto alla media, divisa per il numero dei gradi di libertà della serie. La sua radice quadrata rappresenta la deviazione standard.

12º AMPIEZZA O RANGE:

La differenza tra il valore massimo (è un valore del del campionamento: al di sopra di questo non ci sono valori del campionamento) e minimo (è un valore del campionamento: al di sotto di questo non ci sono valori del campionamento) dei valori di una variabile.

Nell’ampiezza di una variabile si trova compreso il 100% dei valori del campionamento.

Differenza tra il valore massimo e minimo di un campione o popolazione. È valido solo per variabili continue.

13º MISURA DELA DISPERSIONE DI UN CAMPIONE:

È la radice quadrata positiva della varianza.

Se il campione consta di n valori di una variabile y, cioè
, la deviazione standard di y nel campione sarà: , dove y è la media del campione. Tra -1 e +1 deviazioni standard si include un 68,3% delle osservazioni; tra -2 e +2, un 95,4% e tra -3 e +3 praticamente un 99,7%; perciò, in una distribuzione normale ci si aspetta che solo uno 0,3% delle osservazioni realizzate differiscano dalla media in più di tre deviazioni standard.

14º DIFFERENZE STATISTICAMENTE SIGNIFICATIVE:

Le differenze, tra quello che si osserva e quello che si suppone nella ipotesi nulla, non possono essere spiegate con la casualità.

15º DISTRIBUZIONE BIMODALE:

Distribuzione di frequenze con due zone di densità di frequenza (che determinano due mode) separate da una zona intermedia a bassa frequenza di osservazioni.

16º DISTRIBUZIONE BINOMIALE:

Distribuzione della probabilità di osservare x avvenimenti nel corso di n osservazioni indipendenti in cui si suppone, per ogni osservazione, una probabilità p identica che si verifichi l’avvenimento.

Il risultato di ogni test deve essere dicotomico, cioè con due possibilità che si escludano reciprocamente (ad esempio: presenza o assenza della malattia).

17º STUDIO FATTORIALE:

Studio applicato in esperimenti nei quali due o più trattamenti vengono verificati in modo separato o allo stesso tempo, in modo che si possano misurare interazioni tra di loro.

Se l’esperimento riguarda due farmaci o interventi terapeutici A e B, si formano quattro gruppi: uno trattato con A e placebo di B, un altro trattato con b e placebo di A, un altro trattato simultaneamente con A e B, un ultimo gruppo trattato con il placebo di A ed il placebo di B.

18º DISTRIBUZIONE DI FREQUENZE:

Grafico o tabella in cui si mostra la frequenza con cui un valore o caratteristica si presenta in una popolazione o un campione per categorie o sottogruppi.

La sua posizione generale in una scala si descrive con una misura della tendenza centrale; ci sono tre misure di tendenza centrale: la media, la mediana e la moda.

La deviazione standard offre informazioni sulla dispersione del valore misurato nella popolazione studiata.

19º DISTRIBUZIONE DI POISSON:

Distribuzione della probabilità di osservare x episodi di un avvenimento quando ci si aspetta un numero m in un dato periodo.

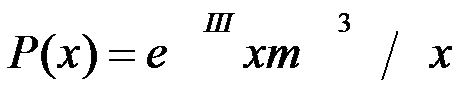la distribuzione di Poisson deriva dalla distribuzione binomiale quando il numero n di osservazioni tende all’infinito (in pratica: quando è superiore a 100) e la probabilità (che si suppone costante in ogni osservazione) di comparsa dell’avvenimento P tende a zero.

La distribuzione di Poisson si utilizza spesso in farmaco vigilanza e farmaco epidemiologia quando si studiano bassi rischi in popolazioni di più di 100 soggetti, allo scopo di calcolare la probabilità di comparsa di un determinato evento, calcolare l’intervallo di confidenza di un tasso, stimare il numero di individui che devono essere inclusi in uno studio, ecc.

20º DISTRIBUZIONE NORMALE O DI GAUSS:

è una distribuzione teorica di probabilità che si usa tanto nella statistica applicata come in quella teorica.

Nella pratica, appare molto frequentemente come conseguenza del risultato importante che stabilisce il teorema centrale del limite.

Ha la forma di una campana ed è caratterizzata unicamente da 2 valori: la media e la varianza.

Distribuzione di frequenze continua, simmetrica, con due code che si estendono all’infinito, in cui la media, la mediana e la moda hanno lo stesso valore e la cui forma è determinata dalla media e dalla deviazione standard.

21º META-ANALISI:

Integrazione strutturata e sistematica dell’informazione ottenuta in studi differenti su un problema determinato.

Consiste nell’identificare e rivedere gli studi controllati su un determinato problema, allo scopo di dare una stima quantitativa sintetica di tutti gli studi disponibili.

Dato che include un numero maggiore di osservazioni, una meta-analisi ha un potere statistico superiore a quello degli esperimenti clinici che comprende.

I due principali problemi metodologici della meta-analisi di esperimenti clinici sono:

1) la eterogenicità degli esperimenti inclusi (nei termini delle caratteristiche cliniche e socio-demografiche delle popolazioni incluse in ogni esperimento, i metodi di valutazione clinica applicati, le dosi, forma farmaceutica o modello di dosaggio del farmaco valutato, ecc).

2) il possibile errore di pubblicazione (derivato dal fatto che non tutti gli esperimenti clinici veramente realizzati sono stati pubblicati).

22º MODELLO LINEARE:

Modello statistico in cui il valore di un parametro y è uguale a a + bx, in cui a (ordinata all’origine) e b (pendente (il cui valore è incluso tra -1 e +1) sono costanti.

23º MODELLO LOGISTICO:

Modello statistico di probabilità della malattia, in funzione di un fattore di rischio x, in cui , dove P (y/x) è la probabilità che appaia e tra i soggetti esposti al fattore x e e è la funzione esponenziale naturale.

Nel modello logistico multiplo, il termine fix viene sostituito da un termine lineare che comprende vari fattori, per esempio:  se esistono due fattori x1 y x2.

24º Livello di significatività:

Nelle prove di significatività statistica, è il valore di p che, in senso stretto, deve essere specificato in anticipo nella fase del progetto.

Il livello accettato con maggiore frequenza è 0,05, ma si possono anche applicare livelli di 0,01 o 0,001, ecc.

25º NUMERO CHE è NECESSARIO TRATTARE (NNT):

Quando il trattamento sperimentale aumenta la probabilità di un accadimento favorevole (o quando diminuisce la probabilità di un avvenimento avverso), è il numero di pazienti che bisogna trattare per ottenere ad un paziente in più con miglioramento (oppure allo scopo di prevenire un avvenimento avverso addizionale).

Si calcola come 1/RAR, arrotondando al numero intero immediatamente seguente, accompagnato da un livello di confidenza al 95%.

26º P (p- valore):

Il livello di significatività osservato nel test.

Quanto più è piccolo, maggiore sarà l’evidenza per rifiutare l’ipotesi nulla.

27º P (probabilità).

Seguita dall’abbreviazione n.s. (non significativa) o dal simbolo < (inferiore a) e una cifra decimale (ad esempio 0,05 o 0,01), indica la probabilità che la differenza osservata in un campione sia occorsa puramente per caso, esseno i gruppi comparati realmente assomiglianti, vale a dire sotto l’ipotesi nulla.

28º PERCENTILE:

Un percentile 90% corrisponde ad un valore che divide il campione in due, in modo che si ha un 90% dei valori del campionamento inferiori a questo valore, ed un 10% di valori del campionamento superiori.

I percentili 25%, 50%, 75% sono il primo, secondo e terzo quartile rispettivamente.

In una serie (sufficientemente grande) di osservazioni ordinate (per esempio da minore a maggiore), la parte che costituisce una percentuale determinata di tutti gli elementi della serie.

Ad esempio: in una serie di valori dell’altezza (in cm), il primo percentile 10 sarà costituito dal 10% degli individui più bassi, metre il decimo percentile 10 sarà costituito dal 10% di soggetti più alti.

Analogamente, il primo quartile o il primo quintile corrisponderanno, rispettivamente, al 25% e al 20% di individui più bassi.

In una distribuzione normale, la mediana corrisponde esattamente al percentile 50 (un 50% degli individui si trovano al di sopra e un 50% di sotto alla mediana).

29 º COEFFICIENTE DI CORRELAZIONE:

Misura di associazione che indica il grado in cui due variabili continue x e y possiedono una relazione lineare (y = a ± bx).

Si designa con la lettera r, ed il suo valore si incontra tra -1 e +1.

I valori di -1 e +1 indicano che esiste una relazione lineare perfetta, negativa o positiva rispettivamente, tra entrambe le variabili, e in una rappresentazione su assi di coordinate i dati si distribuiscono in modo retto, con pendente positiva o negativa rispettivamente.

Quando r = 0, i dati si dispongono in modo circolare e non esiste nessun grado di correlazione.

30º Coefficiente di variazione:

Deviazione standard espressa come percentuale della media, vale a dire (DE/x) X 100.

31º significatività clinica:

Probabilità che una differenza osservata abbia una ripercussione sul decorso del problema o malattia trattata che sia rilevante per un paziente dato o per un gruppo di pazienti.

Non ci si deve confondere con la significatività statistica: sono frequento le descrizioni di differenze statisticamente significative che non sono clinicamente significative.

32º significatività statistica:

Probabilità che una differenza osservata risulti dalla casualità e non dalle determinanti causali di uno studio.

Il riscontro di una significatività statistica non implica necessariamente una significatività clinica.

33º tavola di contingenza:

Tavole di 2 o più variabili, dove in ogni cella si contano gli individui che appartengono ad ogni combinazione dei possibili livelli di queste variabili.

Gassificazione tabulare di dati di un campione di popolazione, in cui le sottocategorie di una caratteristica si indicizzano orizzontalmente (in righe) e quelle di un’altra verticalmente (in colonne).

Così si possono applicare prove di associazione tra le caratteristiche delle righe e delle colonne.

La tavola di contingenza più semplice è quella 2×2, in cui vengono incluse due categorie della caratteristica delle file e due categorie della caratteristica delle colonne (cioè quattro valori).

Per esaminare i risultati di un esperimento clinico, di solito si dispongono nella fila superiore i dati che si riferiscono allo studio sperimentale, in quella inferiore quelli corrispondenti al gruppo di riferimento.

Nella prima colonna di solito si riportano il numero dei pazienti che presentano il fenomeno studiato, nella seconda il numero di quelli che non presentano il fenomeno.